Les représentations planes de la Terre - GÉODÉSIE - CNIG
←
→
Transcription du contenu de la page
Si votre navigateur ne rend pas la page correctement, lisez s'il vous plaît le contenu de la page ci-dessous
GÉODÉSIE
Les représentations planes de la Terre
Françoise DUQUENNE
Depuis l’antiquité on sait que la Terre est ronde ou Les déformations
MOTS-CLÉS Toute projection d’un ellipsoïde sur un
presque. Cependant il s’avère depuis toujours très pratique
Représentations planes, plan induit des déformations. On peut
d’en faire une représentation plane, que ce soit sur
module linéaire, prendre comme image un ballon de
du papier ou de nos jours sur un écran d’ordinateur. On altération linéaire, baudruche que l’on essaie d’aplatir sur
appelle très souvent ces représentations planes de la Terre conforme, équivalente, une table et que l’on va étirer pour arri-
des “projections cartographiques”, terminologie associée cylindrique, conique, ver au résultat, alors on déforme mais
à “carte”, voire à “plan cartésien”. Remarquons ici qu’elles indicatrice de Tissot pas de la même façon partout. Autre
ne sont pas toutes des projections au sens mathématique analogie la peau d’une orange que l’on
et géométrique du terme. Il existe de nombreuses représentations planes veut aplatir sur la table, et qui va se
déchirer jusqu’à ce que les morceaux
et nous nous proposons ici, non pas d’en faire un inventaire mais de présenter
puissent être aplatis avec des déforma-
leurs caractéristiques, de voir comment on peut les classer et comment on les choisit tions très petites et non déchirantes.
selon leur utilisation. Pour représenter la Terre entière, donc
à des échelles très petites, on va plutôt
Qu’est-ce Un point de laTerre qui est sur la surface
procéder comme pour le ballon de
qu’une représentation topographique est repéré par ses coor-
baudruche, tandis que pour les grandes
plane de la Terre données géographiques : longitude (λ),
ou moyennes échelles (ex. : 1/5 000,
latitude (φ) et hauteur (h).
1/25 000, etc.) on va découper laTerre en
On choisit tout d’abord une forme La première étape consiste à projeter le
zones, correspondant à un continent, un
géométrique approchée de la Terre point sur l’ellipsoïde en un point Mo qui
pays, à des zones plus petites délimitées
débarrassée de ses reliefs. Lorsque a les mêmes longitude et latitude que
par des méridiens et des parallèles. Pour
l’on veut faire une représentation le point M.
chacune de ces zones, on définira une
à très petite échelle (par exemple La deuxième étape est une transforma-
projection et ses paramètres qui feront
1/100 000 000) on choisit une sphère, tion de l’ellipsoïde en plan, en réalisant
le moins de déformation.
tandis que pour les cartes à moyennes une application qui à toutes coordon-
Les longueurs sont toujours altérées
et grandes échelles on utilise un ellip- nées (λ, j) du point fait correspondre
car la sphère ou l’ellipsoïde ne sont
soïde de révolution. Leurs dimensions des coordonnées du plan cartésien
pas développables sur un plan et pour
proches de 6 400 km pour le rayon d’une (x,y). L’application réciproque existe. En
quantifier cette déformation on intro-
sphère et un aplatissement proche de général l’expression mathématique est
duit le module linéaire :
1/300 pour un ellipsoïde, diffèrent de la forme
de plusieurs centaines de mètres.
Avec ds élément de longueur infinité-
Historiquement quelques sphères
simal sur l’ellipsoïde et dS l’élément
(sphère de Picard : R=6371598 m) et de Remarque : le plus souvent, mais pas
correspondant sur le plan.
nombreux ellipsoïdes (Clarke, Hayford, systématiquement, l’axe x est dirigé
Bessel, Krakovski…) ont été utilisés. La vers l’Est et y vers le Nord et les coor-
Figure 2. Abscisse
tendance actuelle est de choisir quelle données (x,y) se notent aussi (E,N) pour
curviligne
que soit l’échelle de la carte l’ellipsoïde easting et northing.
sur l’ellipsoïde
WGS84 ou ce qui est équivalent à mieux Ces fonctions peuvent être très compli-
que le millimètre l’ellipsoïde internatio- quées mais aussi très simples comme
nal GRS80. par exemple la représentation plate
carrée (Figure 4) qui était déjà utilisée
par Eratosthène (273-192 av. J.-C.) bien
que la latitude et longitude n’étaient pas
utilisées à cette époque.
où a est le rayon de la sphère
représentant la Terre
Figure 1. Principe d’une représentation plane
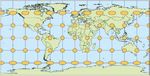
36 Revue XYZ • N° 156 – 3e trimestre 2018Les représentations pour lesquelles Ainsi on voit que pour la projection
m1 m2 = 1 en tout point sont dites équi- “plate carrée”(Figure 4), sur l’équateur
valentes. Elles conservent les surfaces l’indicatrice de Tissot est un cercle, puis
car la surface de l’ellipse pm1 m2 = p est en se déplaçant vers les pôles l’indi-
égale à la surface du cercle de rayon 1. catrice de Tissot s’aplatit et s’élargit, il
Les représentations qui ne sont ni y a une dilatation des zones polaires.
conformes, ni équivalentes sont dites Cette projection n’est ni conforme, ni
aphylactiques. équivalente. Les images des parallèles
Figure 3. Abscisse curviligne sur le plan
étant à égale distance on dit qu’elle est
Les figures 4, 5, 6 et 7 montrent des
équidistante. La projection Mercator est
exemples de projections pour lesquelles
un exemple de projection conforme.
on voit les images des méridiens et de
L’indicatrice de Tissot est un cercle quel
parallèles et au croisement on a figuré
que soit le lieu, et ce cercle devient
les indicatrices de Tissot.
de plus en plus grand quand on se
rapproche des pôles. La déformation
des longueurs est la même dans toutes
les directions en un lieu donné mais
son amplitude augmente avec la lati-
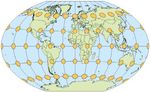
tude. Pour la projection de Mollweide
(Figure 6) l’indicatrice de Tissot est une
ellipse dont le grand axe est dirigé selon
Figure 4. Plate carrée : cylindrique l’image du méridien. L’ellipse s’aplatit
équidistante en s‘approchant des pôles mais garde
une aire constante. Cette projection
est équivalente. Aucune représenta-
tion plane de l’ellipsoïde n’est à la fois
conforme et équivalente. Par contre on
Le module linéaire peut comme dans le cas de la projec-
tion de Winkel-Tripel faire en sorte que
est donc une fonction de (λ, j) qui les déformations soient minimisées, ici
dépend de la position du point et de la l’indicatrice est presque un cercle dont
direction dans laquelle on regarde la l’aire varie peu.
déformation.
En un point de coordonnées (λ, j) varie Image du canevas
entre deux valeurs : m1 < m < m2 La valeur
maximale m2 peut être infinie ∞. Les méridiens et les parallèles qui sur
On appelle altération linéaire la quantité la sphère ou sur l’ellipsoïde sont des
e = m -1 exprimée souvent en mètres par cercles ou des ellipses peuvent être
Figure 5. Mercator : cylindrique conforme
kilomètres. transformés par la représentation en
On appelle isomètre une courbe telle toutes sortes de courbes. Il est habi-
qu’en tout point m = constante. Si m = 1 tuel de procéder à une classification
elle est dite automécoïque. des représentations planes selon ces
Pour visualiser les déformations courbes de la manière suivante :
on utilise l’indicatrice de Tissot. On
Les représentations cylindriques : les
trace sur l’ellipsoïde un petit cercle
images des parallèles sont des droites
de rayon 1 (l’unité importe peu), la
parallèles et celles des méridiens des
transformée de ce cercle par la repré-
Figure 6. Mollweide : méri-cylindrique droites parallèles perpendiculaires aux
sentation plane est toujours une ellipse
premières (Figure 4, 5, 9).
de demi-grand axe m2 et de demi-petit q
axe m1, c’est l’indicatrice de Tissot. Les
représentations pour lesquelles m1 = m2
en tout point sont dites conformes, l’in-
dicatrice de Tissot est un cercle. Elles
ont deux intérêts, le premier c’est que
l’altération linéaire en un point est la
même dans toutes les directions, et le Figure 8.
deuxième les angles sont conservés représentation
Figure 7. Winkel-Tripel
dans la transformation. cylindrique [5]
Revue XYZ • N° 156 – 3e trimestre 2018 37GÉODÉSIE
Par analogie, c’est comme si on enve-
q loppait la sphère par un cylindre que
l’on dépliait ensuite, mais attention la
transformation n’est pas en général une
projection géométrique.
Figure 13. Conique équivalente
Figure 9. Cylindrique équivalente Les projections méri-coniques (ou
pseudo-conique) : les images des Figure 16. Polyconique
Les projections méri-cylindriques (ou parallèles sont des arcs de cercles
pseudo-cylindriques) : les images des concentriques, celles des méridiens L’aspect
parallèles sont des droites parallèles, sont des courbes quelconques passant
celles des méridiens sont des courbes par l’image du pôle. Pour illustrer l’aspect, prenons
(arc de cercle, arc de sinus (Figure 10), l’exemple des projections cylin-
Les projections azimutales (cas parti-
arc d’ellipse (Figure 6), etc.) driques. On dit que la projection est
culier de conique) : les images des
directe lorsque l’axe du cylindre est
parallèles sont des cercles concen-
confondu avec l’axe des pôles, elle
triques, celles des méridiens sont des
est oblique lorsque l’axe du cylindre
droites concourantes au centre des arcs
est incliné selon une direction qu’on
de cercles qui est aussi l’image du pôle
appelle axe des pseudo-pôles, et
(nord ou sud) (Figure 15).
transverse lorsque l’axe du cylindre
est dans l’équateur. On associe à l’axe
Figure 10. Sanson : méri-cylindrique des pseudo-pôles un pseudo-cane-
sinusoïdale vas, composé de pseudo-parallèles
et pseudo-méridiens. On applique au
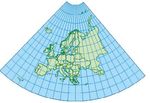
Les projections coniques : les images
pseudo-canevas la classification vue
des parallèles sont des arcs de cercles
précédemment, par exemple pour
concentriques, celles des méridiens
une projection cylindrique oblique les
sont des droites concourantes au centre
pseudo-méridiens et pseudo-parallèles
des arcs de cercles qui est aussi l’image
seront des droites perpendiculaires
du pôle (nord ou sud) (Figures 12, 13).
les unes aux autres, ce qui n’est pas
Par analogie, c’est comme si on enve-
le cas pour les méridiens et parallèles.
loppait la sphère par un cône que l’on Figure 14. Représentation azimutale [5]
Mathématiquement on applique les
dépliait ensuite, mais attention la trans-
mêmes fonctions mais en utilisant les
formation n’est pas en général une
pseudo-longitudes et pseudo-latitudes
projection géométrique.
(coordonnées Cassini-Soldner). On
peut aussi appliquer l’aspect oblique
Figure 11. Représentation aux représentations coniques et azimu-
conique [5] tales.
Figure 15. Azimutale équivalente
Figure 12. Conique
Les projections poly-coniques : les
conforme
images des parallèles sont des arcs
Figure 17. Aspect direct et oblique
de cercles non concentriques, dont le
centre est situé sur une droite, image On distingue aussi les représentations
du méridien origine, et les images des sécantes et tangentes : en reprenant
autres méridiens sont des courbes quel- l’analogie, dans le premier cas le cône
conques (Figure 16) ou le cylindre coupe la sphère, et dans
38 Revue XYZ • N° 156 – 3e trimestre 2018Figure 18. Aspect sécant et tangent
l’autre cas il est tangent. Ce que l’on
peut exprimer dans le premier cas, il
existe deux isomètres automécoïques
(m = 1) et dans le deuxième il n’y en a
qu’une.
Le nom des
représentations planes
Certaines représentations peuvent Figure 20. Le Monde 2008 – projection cylindrique équivalente (Peters)
être nommées à l’aide de leurs carac-
Quelles projections pour l’importance des pays en superficie et
téristiques, comme par exemple la
sont très utiles pour des cartes théma-
projection conique conforme, mais quelles applications ?
tiques : par exemple si on représente
souvent elles portent le nom de leur
n Cartes du monde (Atlas) le nombre d’habitants d’un pays par
inventeur, Lambert pour la même
Les cartes du monde que l’on trouve un cercle dont le rayon dépend de la
projection. On peut citer les noms
dans les Atlas peuvent être choisies population, pour avoir une impression
fréquemment rencontrés : Aïtoff,
selon divers critères. L’esthétique en est de densité réaliste, il faut conserver le
Albers, Bonne, Cassini, Eckert, Gauss,
un, la projection de Molweide (Figure 6) rapport des superficies des pays. En
Gall, Guillaume Postel, Hammer, Hatt,
par exemple est souvent choisie, car sa général le haut de la carte est vers le nord,
Goode, Krüger, Laborde, Lorgna,
forme rappelle celle de la Terre, tandis mais il existe des cartes ayant le sud en
Lambert, Mercator, Miller, Mollweide,
que celle de Sanson (Figure 10) est plus haut. De même le méridien central n’est
Peeters, Sanson, Soldner, Wagner,
originale. Les projections équivalentes pas toujours le méridien de Greenwich.
Winkel. Il est évidemment plus pratique
sont très utilisées, car elles respectent La carte du monde (Figure 14) est centrée
d’utiliser la première méthode de dési- q
gnation d’une projection, d’autant que
plusieurs noms peuvent représenter la
même projection, comme par exemple
la représentation cylindrique équidis-
tante qui s’appelle Cassini ou Soldner
selon le pays. Par ailleurs un même
nom peut être utilisé pour des projec-
tions différentes, comme Lambert pour
les projections coniques conforme et
équivalente. Certaines projections sont
obtenues par une perspective géomé-
trique sur un plan, un cône ou un
cylindre tangent à la sphère, et selon
le point de vue qui peut être le centre
de la sphère, un pôle, l’infini, elles sont
appelées gnomoniques, stéréogra-
phiques, ou orthographiques.
Figure 19. Projections gnomonique,
stéréographique, orthographique. Figure 21. Carte du pôle nord (1880) : projection azimutale
Revue XYZ • N° 156 – 3e trimestre 2018 39GÉODÉSIE
parallèles,
le trajet à cap constant (loxo-
dromie) entre deux lieux est représenté
par une droite. Par contre le trajet le
plus court (orthodromie) est une courbe
dont la courbure peut être grande. La
figure 24 montre les deux trajets entre
Berlin et Tokyo. Cet exemple illustre
bien le fait qu’une ligne droite sur une
carte n’est pas forcément le chemin le
plus court. La projection de Mercator
déforme malheureusement beaucoup
les zones polaires, son utilisation est
limitée entre les latitudes – 60° et + 60°.
Une autre projection est souvent utili-
sée pour figurer les trajets des avions
de ligne, c’est la projection azimutale
oblique. En effet les avions en principe
suivent le chemin le plus court (géodé-
sique) et donc des arcs de grands
cercles sur une sphère. Pour figurer
tous les vols à partir d’un aéroport,
on peut utiliser une projection oblique
de pseudo-pôle le lieu de départ.
Dans cette projection tous les cercles
passant par le pseudo-pôle sont des
droites donc tous les trajets à partir de
Figure 22. Carte de l’Antarctique (1972) projection azimutale oblique (Lorgna)
cet aéroport sont des droites. Si de plus
on choisit la projection équidistante,
sur le méridien de longitude 150° et est de combiner ces deux types de projec-
q orientée le sud en haut. tions (Figure 23).
alors la longueur de chaque trajet est
conservée.
Les projections cylindriques repré-
sentent bien les zones équatoriales, ou n Les cartes pour la navigation
de latitudes moyennes, mais les zones La navigation a toujours été un objec-
polaires sont soit très dilatées, soit très tif majeur des cartes et l’on doit les
écrasées. Par contre les projections premières cartes à des grands naviga-
azimutales représentent bien les zones teurs. La projection de Mercator, utilisée
polaires (Figure 15, 21). L’aspect oblique depuis le XVIe siècle est la préférée
est aussi souvent utilisé (Figure 22). Il est des navigateurs. Elle est conforme, et
donc fréquent pour une carte du monde comme les méridiens sont des droites
Figure 24. Projection de Mercator : trajets
loxodromique et orthodromique
n Les cartes topographiques
Les cartes topographiques sont des
cartes à moyenne ou à grande échelle.
La projection est appliquée à une zone
qui correspond par exemple à un
pays, ou même le pays est découpé
en zones selon des parallèles ou
des méridiens afin de représenter
les détails topographiques avec le
moins de déformations possibles. On
utilise alors la même projection mais
avec des paramètres différents. Les
techniques de levés topographiques
consistent en particulier à mesurer des
Figure 23. Carte du pacifique combinant deux projections : une azimutale et une cylindrique angles et des distances, les projections
40 Revue XYZ • N° 156 – 3e trimestre 2018utilisées sont conformes, ce qui permet – En toute rigueur, S est donné par tion m1m2 est considéré comme égal
de conserver les angles mais aussi les l’intégrale curviligne : à l’angle entre l’ellipse méridienne
longueurs étant déformées de la même vers le nord et la ligne géodésique.
façon dans toutes les directions, il est En projection conforme, l’azimut est
facile de corriger les distances mesu- – Pour une distance courte (quelques conservé, c’est l’angle entre l’image
rées pour les reporter sur la carte. Les centaines de mètres), m peut être du méridien et l’image de la géodé-
projections les plus utilisées sont la considéré comme constant : sique (courbe M 1M 2 sur la partie
conique conforme, les cylindriques droite de la figure).
conformes obliques ou transverses, et – Pour des distances plus longues, il – Pour utiliser les formules classiques
la projection stéréographique (azimu- est nécessaire de calculer une valeur de la géométrie plane, il faut corriger
tale conforme) oblique. moyenne du module linéaire : l’azimut du petit angle entre l’image
de la géodésique et le segment de
Les représentations conformes possè-
droite M1M2. Cette correction est notée
dent des propriétés particulières qui
– Pour les distances très longues dV, on l’obtient à partir de rg, rayon
vont faciliter la réduction des oberva-
(plusieurs dizaines de kilomètres), on de courbure de l’image de la géodé-
tions d’angles et de distances faites sur
utilise la formule des trois niveaux, sique. Celle-ci tourne sa concavité
le terrain
qui nécessite le calcul du module vers l’isomètre centrale, vers laquelle
– L’indicatrice de Tissot est un cercle.
linéaire aux deux extrémités et au se trouve donc le centre de courbure
– Le module linéaire ne dépend que de
milieu de l’arc de géodésique : C. On appelle isomorphes les courbes
la position du point.
orthogonales aux isomètres, et on
– L’altération angulaire est toujours
note Sv leur abscisse curviligne. La
nulle.
distance entre deux isomètres d’équa-
– On note m0, la valeur minimale du – U ne transformation conforme
tions m = Cste et m + dm = Cste est donc
module linéaire. En un point quel- conserve les angles. Cependant,
la différentielle de l’abscisse curviligne
conque on a m0 ≤ m ≤ ∞. l’image plane d’une ligne géodé-
sur l’isomorphe, dSv. On désigne par
– L’isomètre dont le module linéaire sique de l’ellipsoïde n’est en général
i l’angle entre l’isomorphe et l’image
vaut m0 est choisie au centre de la pas une géodésique du plan (une
de la géodésique. rg est donné par la
zone à cartographier et est nommée droite), mais une courbe tournant
formule de Schols :
isomètre centrale. sa concavité vers l’isomètre centrale
– On choisit m0 < 1 et donc il existe (figure 26). Ceci entraîne qu’une (1)
nécessairement des isomètres pour petite correction doit être apportée
lesquelles m = 1. Elles sont automé- aux angles horizontaux observés - On peut montrer que, comme rg n’est
coïques. Au voisinage de l’isomètre avant de les utiliser pour des calculs pas rigoureusement constant entre
centrale, en un point m à distance planimétriques. Sur la partie gauche M1 et M2, il convient de le calculer
d de celle-ci, le module linéaire se de la figure 26, l’azimut de la direc- pour le point M1/3 situé sur l’image
développe sous la forme : de la géodésique au tiers de M1M2.
On a ensuite :
où p dépend un peu du point m et où
o(d2) est un infiniment petit d’ordre
supérieur à d2.
q
- Soit s la distance séparant deux points
m1 et m2 de l’ellipsoïde (figure 25). La
distance correspondante en plan est
S. Si l’arc de courbe sur l’ellipsoïde est
une géodésique, son image plane est
peu courbée et, sur le plan, on peut
confondre la longueur de l’image
de la géodésique et la longueur du
segment M1M2.
Figure 26. Transformation conforme
d’une géodésique de l’ellipsoïde.
Figure. 25. Réduction d’une distance de
l’ellipsoïde au plan.
Revue XYZ • N° 156 – 3e trimestre 2018 41GÉODÉSIE
– S uivant la précision requise, la Les cartes des figures 2, 3, 4, 5, 6, 7, 8,
q ABSTRACT
projection utilisée, la longueur des 9, 10, 11, 18, 19, 21 ont été générées
visées et l’éloignement de l’isomètre par les logiciels et données Mapinfo This paper presents a general view
centrale, il convient de contrôler si dV et Arcgis. of the representations of the Earth
peut être négligé. onto a plane surface. Booth the
Remerciements à Bernard Bèzes, ex
mathematical characteristics of the
responsable de la cartothèque de l’IGN
n Convergence des méridiens projections and their geometric
qui a fourni les cartes de la collection
Les images des méridiens peuvent être characteristics, including projected
IGN des figures 14, 15, 16, 17.
très variées, droites parallèles, droites images of the meridians and
sécantes, cercles, courbes quelconques. parallels, are highlighted. Then
On choisit un méridien origine, comme Références the direct and inverse aspects
axe des y, et en un point quelconque are explained as well as the
[1] Bugayevskiy M. Snyder J., 1995, Map
l’image du méridien fait un angle γ avec
Projections, Taylor&Francis classifications by purpose of use,
l’axe des y qu’on appelle convergence such as world atlas, navigation
[2] Duquenne F. et H., 2003, cours de
des méridiens. and surveying. The notions of scale
géodésie, ESGT, CNAM. http://www.aftopo.
factor, convergence of meridians and
org/FR/ouvrages-34.html
reduction to the chord are explained.
[3] Duquenne F., Les projections The paper will be completed in
cartographiques, bulletin de liaison des detail within the next issues by the
membres de la Société de Géographie studies of projections mostly used in
n°18, juin 2012. surveying.
[4] Reignier F. 1957, Les systèmes de
projections et leurs applications, IGN
[5] www.regard-sur-la-terre.over-blog.com
Figure 27. Passage azimut vers gisement
VM1M2 : gisement : angle entre l’axe des
Y et la direction M1M2
AzM1M2 : azimut : angle entre le méridien
et la direction M1M2
γ : convergence de méridiens = gise-
ment de l’image du méridien.
Conclusion
Ces quelques pages ont résumé les
façons les plus répandues de repré-
senter la Terre sur un plan. Cependant
il en existe de nombreuses autres et
l’imagination n’a pas de limite. On
peut prendre ici comme exemple la
carte anamorphique de la SNCF qui à
la place des distances, utilise la durée
des trajets des trains.
Cet article dont le but est une vue
générale sur les représentations
planes de la Terre sera complété ulté-
rieurement dans la revue XYZ par
l’étude détaillée des représentations
planes les plus utilisées en topogra-
phie et cartographie, en particulier
les représentations légales françaises
et celles spécifiées dans la directive
européenne INSPIRE. l Figure 28. Carte anamorphique de la SNCF
42 Revue XYZ • N° 156 – 3e trimestre 2018Vous pouvez aussi lire